1、实验题目
2、实验目的
了解激光散斑的统计特性，学会两种处理激光散斑的重要方法：自相关函数法和互相关函数法。
3、实验器材：
氦氖激光器，可调衰减器，扩束器，透镜，毛玻璃，CCD，计算机。
4、实验原理
激光散斑的基本概念：激光自散射体的表面漫反射或通过一个透明散射体（例如毛玻璃）时，在散射表面或附近的光场中可以观察到一种无规分布的亮暗斑点，称为激光散斑（Laser Speckles）或斑纹。如果散射体足够粗糙，这种分布所形成的图样是非常特殊和美丽的（对比度为1）。
激光散斑是由无规散射体被相干光照射产生的，因此是一种随机过程。要研究它必须使用概率统计的方法。通过统计方法的研究，可以得到对散斑的强度分布、对比度和散斑运动规律等特点的认识。
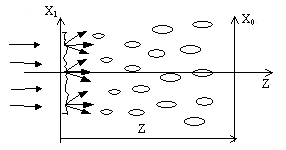
图1 光散斑的产生(图中为透射式，也可以是反射式的情形)
图1说明激光散斑具体的产生过程。当激光照射在粗糙表面上时，表面上的每一点都要散射光。因此在空间各点都要接受到来自物体上各个点散射的光，这些光虽然是相干的，但它们的振幅和位相都不相同，而且是无规分布的。来自粗糙表面上各个小面积元射来的基元光波的复振幅互相迭加，形成一定的统计分布。由于毛玻璃足够粗糙，所以激光散斑的亮暗对比强烈，而散斑的大小要根据光路情况来决定。散斑场按光路分为两种，一种散斑场是在自由空间中传播而形成的（也称客观散斑），另一种是由透镜成像形成的（也称主观散斑）。在本实验中我们只研究前一种情况。当单色激光穿过具有粗糙表面的玻璃板，在某一距离处的观察平面上可以看到大大小小的亮斑分布在几乎全暗的背景上，当沿光路方向移动观察面时这些亮斑会发生大小的变化，如果设法改变激光照在玻璃面上的面积，散斑的大小也会发生变化。由于这些散斑的大小是不一致的，因此这里所谓的大小是指其统计平均值。它的变化规律可以用相关函数来描述。
n激光散斑光强分布的相关函数的概念：
l自相关函数
假设观察面任意两点上的散斑光强分布为Ｉ(x1,y1)，Ｉ(x2,y2)，我们定义光强分布的自相关函数为：
其中Ｉ(x1,y1)表示观察面上任一点Q1的光强，Ｉ(x2,y2)表示观察面上另一点Q2上的光强，〈〉表示求统计平均值。根据光学知识我们知道：
式中U(x,y)表示光场的复振幅。当玻璃板表面足够粗糙（毛玻璃）时,根据散斑统计学的理论我们可以得到如下的公式：
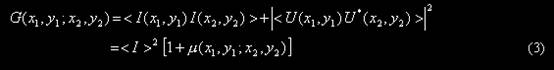
式中m(x 1,y1；x2, y 2）=|〈U(x 1, y 1) U*(x 2, y 2) 〉|2¤〈Ｉ〉2称做复相干系数。由于激光器出射的光斑为高斯分布的（参见6.1），根据衍射理论可推出其复相干系数（推导方法用菲涅尔衍射公式，参见6.2）为：
式中Dx=(x2-x1)，Dy=(y2-y1)，(3)式化为：
进行归一化处理，可以得到归一化的自相关函数为：
其中S的意义即代表散斑的平均半径。从6.2中可以知道S与激光高斯光斑半径W（在毛玻璃上的光斑）的关系式为
因此测量出S的大小就可以求出W。
l两个散斑场光强分布的互相关函数
假设观察面任意一点Q1上的散斑光强分布为Ｉ(x1,y1)，当散射体发生一个变化后（如散射体发生一个微小的平移
）观察面任意一点Q2上的散斑光强分布为Ｉ’(x2,y2) 我们定义光强分布的互相关函数为：
同上面一样有：
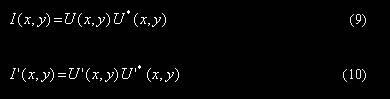
式中U(x,y)和U‘(x,y)分别表示两个散斑光场的复振幅。还是根据散斑统计学的理论我们可以得到如下的公式：
式中mC(x1,y1；x2,y 2)=|〈U‘(x 1, y 1)U*(x 2, y 2)|2¤〈Ｉ〉2称作复互相干系数。根据衍射理论可推出其复相干系数（推导方法用菲涅尔衍射公式，参见6.3）为：
式中Dx = (x2-x1)，Dy = (y2-y1)
所以，两个散斑场的互相关函数为：
进行归一化处理，可以得到归一化的互相关函数为：
5、实验内容
5.1 激光散斑照相实验
1.1、根据激光散斑照相实验装配图安装所有的器件，将导轨用M6螺钉固定在光学平台上。
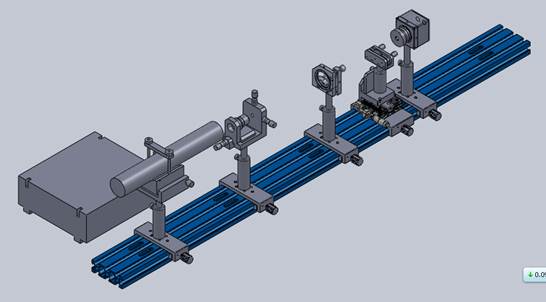
激光散斑照相实验
注意：在安装CMOS相机时，请根据螺纹螺距区分英制与公制螺纹孔，如需要使用英制1/4”-20螺纹孔连接CMOS时，请使用英制-公制螺纹转接头，如下图：
1.2、将所有器件调整至同心等高。
1.3、打开并调整激光器，使发射的激光水平，在光路中放入空间滤波器，在调整空间滤波器之前，先去掉针孔，当物镜出射的光斑中心沿水平方向时，调节完毕。放入针孔，推动物镜旋钮靠近小孔，推动过程中，不断调整小孔位置使得透射光斑最亮，光通过滤波器后检查射出的光点是最亮的，无衍射条纹，光斑变得均匀时，说明已经调好。
1.4、使用平凸透镜将激光光束准直，观察光斑远近大小尺寸，调节平凸透镜与空间滤波器的距离。当光斑在远近处直径一致时，认为光束准直完成。
1.5、调节毛玻璃的位置与高低，使光斑照射在完全毛玻璃上。
1.6、打开相机的采集程序，使用连续采集模式。调节相机的位置与高低，使光照射在相机的适当位置上。此时如果显示图像亮度过高适当减小相机的增益值和快门速度。（注：尽量缩进相机与毛玻璃的距离）
1.7、采集并保存此时相机上的图像。
1.8、转动精密平移台上的千分尺，使毛玻璃向左右移动一定位置，（例如
1.9、更换不同的位移量，重复上步骤3次，点击打开软件“LESPI”。
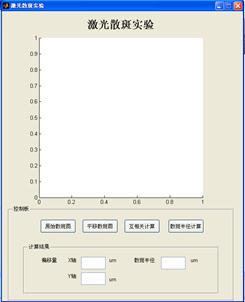
1.10、点击“原始散斑图”，按照路径选择原始图片，点击“平移散斑图”，按照路径选择位移后图片。
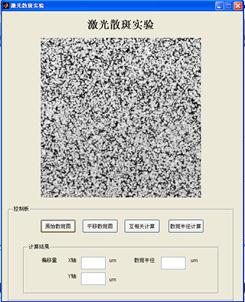
1.11、点击“互相关计算”进行计算，测出其偏移量。
1.12、，然后点击“散斑半径计算”，计算得出散斑半径。
1.13、转动侧升降台上的千分尺，重复步骤8~12，比较毛玻璃竖直移动位移和软件输出结果之间的差距。
5.2 激光散斑照相实验
2.1、根据激光散斑照相实验装配图安装所有的器件。
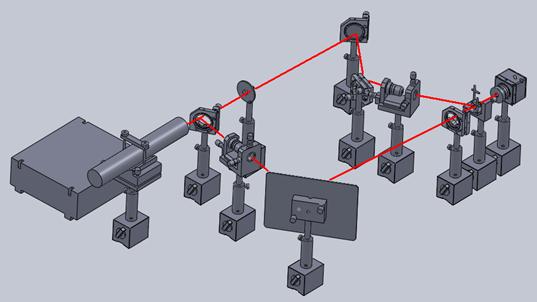
激光散斑照相实验
2.2、将所有器件调整至同心等高。整激光管夹持器水平，固定可变光阑的高度和孔径，使出射光在近处和远处都能通过可变光阑。注：固定可变光阑高度，此可变光阑将在以下实验步骤中作为光路调整高度标尺。
2.3、调节白屏、双胶合透镜、相机，使得相机清晰的采集到白屏上图像，调节相机的曝光时间和增益，使图像亮度合适。（注：为简化实验操作，可在白屏上悬挂一张较多字迹的白纸，相机能采集到清晰的文字时即可）。
2.4、取下2个空间滤波器，打开激光电源，将衰减片调节到透视最大，调节分光光楔、反射镜、分光棱镜，使分光棱镜分出的光打到相机上的同一位置。
注：分光光楔安装时，请尽量保证楔角所在平面与水平面平行。这时透射和反射光将不会发生上下方向偏折。
2.5、用卷尺测量参考光光程与物光光程，如果这两个光程不等，适当调节反射镜的位置，使这两个光程大致相等。
2.6、插入空间滤波器，使用可变光阑作为高度标尺，调整空间滤波器的高度（不加针孔），使得激光通过显微物镜后的扩束光斑中心与可变光阑中心重合，此时锁定空间滤波器高度，及平移台水平移动旋钮；加入针孔，旋转螺纹付推动物镜靠近针孔，在此过程中不断调整针孔位置旋钮，保证透过光的光强最大，当透过光无衍射环且光强最强时，空间滤波器调整完毕。调整作为准直用的平凸透镜与空间滤波器的距离，使出射光的光斑在近处和远处直径大致相等。固定可变光阑位置。
2.7、比较参考光与物光光强，通常情况下，参考光光强较强，适当调节圆形可调衰减器，使参考光与物光光强大致相等。
2.8、采集并保存此时相机上的图像。
2.9、微调可调棱镜支架，采集并保存变化后相机上的图像。
2.10、重复上步骤5次，点击打开软件“ESPIRL”。
2.11、单击“原始图样”，按照路径选择原始图片，再点击“位移图样”，按照路径选择位移后图片。
2.12、点击“散斑计算”，进行计算。所得的偏转角为毛玻璃水平移动位移的绝对值。
2.13、重复上步骤，计算5张图中每相邻的两张图。
6、附录
6.1 激光高斯光束的传播特点
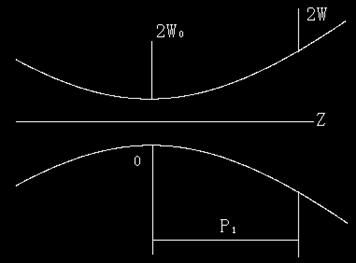
本实验中用长
其中α=λ/πW02，r(Z)为高斯光束在距离束腰Z处的波面曲率半径。在该处光场的复振幅分布为：
6.2 激光高斯光束通过毛玻璃后形成的散斑场的自相关函数的推导
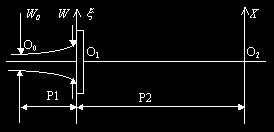
光路原理图
O1x轴位于毛玻璃的前表面上（O1h轴垂直纸面向外），O2X轴位于观察平面（即为CCD的接受平面,O2Y轴垂直纸面向外）上。激光高斯光束从激光器射出，沿光轴O0(O1)O2方向入射到毛玻璃上，其束腰位置为O0，束腰半径为W0，从O0到O1x位置的距离等于P1从O1x位置到O2X位置的距离等于P2，由6.1公式(3)可知高斯光束到达毛玻璃平面上时其光强分布的表达式为：
以下省略因子exp(j2pZ0/l)，因为这项对光强大小无影响。设毛玻璃为无吸收位相物体，其位相分布为F(x，h)，当它表面的起伏远远大于一个波长且在一个可以分辨的小区域中包含很多的起伏的结构时，可以用狄拉克函数来表示毛玻璃上任意两点的关系：
〈〉表示系综平均。由于F(x)为平稳随机过程，所以在具体实验中(2)式总是成立的。当激光束从毛玻璃后表面透射出来，光场的复振幅用下式来描述：
由菲涅尔衍射公式可以计算出此光场再传播一段距离P2到达观察屏上的光场的复振幅分布：
定义μ(x1 , y1 ; x2 , y2)为复相干系数：
其中*代表复共轭，<I>表示散斑场光强的平均值，利用d函数的筛选性质
完成统计平均和积分运算就可以得到
其中Dｘ=|ｘ1-ｘ2| ， Dｙ=|ｙ1-ｙ2 |，S与W的关系式为:
6.3 关于毛玻璃移动前后两个散斑场的互相关函数与毛玻璃位移量的关系的公式
可以证明：
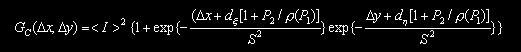
而且X和Y的结果在形式上完全相同。所以为了计算比较简单起见，以下我们用一维的方式进行演算。
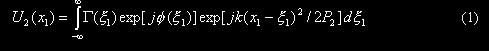
当毛玻璃沿x移动一个小量d0x，则可以肯定在观察屏上的光场的复振幅分布将发生变化，
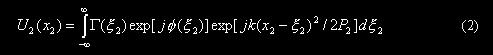
所以在观察屏上由毛玻璃发生移动而产生的两个光场（即散斑场）的光强分别为：
移动前，
移动后，
由这两个光强分布求得它们的互相关函数。由散斑统计的原理[5]可知，U2(x1),U
下面令
将(1)、(2)式代入(6)并求统计平均和积分，由概率论公式和d函数的筛选性质(与6.2完全相同)，经运算得：
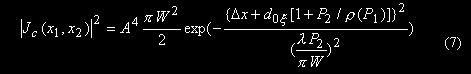
因为
将(7)式代入(8)式得到mc (Dx,Dy)的具体表达式，
其中高斯函数半宽度为S=lP2/pW（即散斑的统计平均半宽度），高斯函数的峰值位置为
½Dx½=d0x（1+ P2/r（P1））
½Dy½=d0h（1+ P2/r（P1））
6.4 经过透镜的高斯光束束腰位置和大小的推导
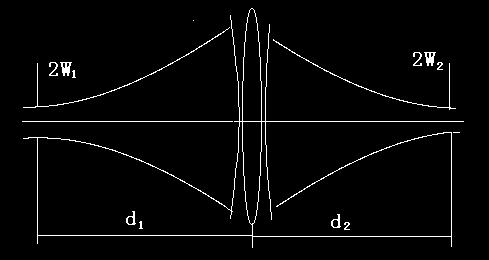
设Z1 为 高斯光束束腰W01 到透镜的距离，由近轴条件下高斯光束在介质中的传播规律―ABCD定律[11]可知：
这里q 表示激光束的复曲率半径：
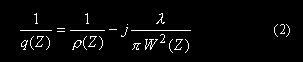
式中r(Z)表示高斯光束波面的曲率半径，W(Z)表示高斯光束的半宽度。
实验中到达透镜表面的高斯光束的波面的复曲率半径为：
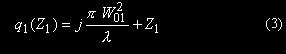
经过透镜后变换为新的高斯光束的束腰位置在透镜后方距离为Z2 处，在此处波面的复曲率半径为：
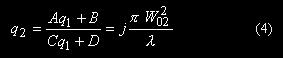
其中A=1-Z2/f，B= Z2，C=-1/f，D=1。将A、B、C和D的值代入（4）式，并比较等式两边的实部和虚部的值就可以求出透镜后高斯光束的束腰位置和大小的理论值：
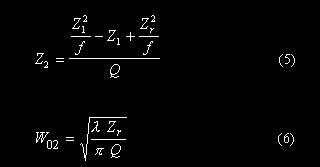
其中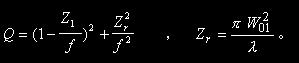
。
利用ABCD定律也可以推导出经过透镜的高斯光束束腰位置和大小的公式，设d1为高斯光束束腰W01到透镜的距离，由ABCD定律可以推导得到经过透镜后高斯光束束腰W02和高斯光束束腰W02 到透镜的距离d2。
（以上内容的详细推导请参见潘笃武等编《光学》上册，p312-330，复旦大学出版社）
6.5 实验数据处理及误差的计算公式和方法
为了简明起见用一维函数的形式说明：
n 由CCD的每一个像元采集到像元所在位置的光强值a(i) ,i=1，2，……，N0。得到激光散斑场的光强分布情况(如正文图2所示)。为了求出散斑半宽度的统计平均值，我们采用求a(i)的自相关函数的方法[5]。公式为：
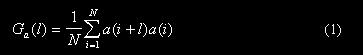
其中N=N
Dx=lds，ds =
n 拟合的具体方法如下：将(2)式中右边的常数a移到左边，然后两边取对数， 得到下式：
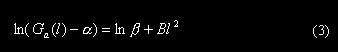
令ln(Ga(l)-a) = y，A = lnb，(3)式可以化为y = A+Bl2的形式。B = -1/S2，l=0,1,¼,Lmax。于是(3)式就可以按最小二乘法进行拟合。(这里较困难的问题是a的数值的确定，目前采用的是取实验曲线的第一极小点或第一拐点。在本实验中对于满足深随机屏[3]的毛玻璃一般情况下都可以得到较好的拟合效果。)
n 互相关函数GC(l)的实验曲线的表达式如下：
可以通过寻找最大值的方法找到峰值位置D，也可以按上面类似的方法进行拟合求出散斑的半宽度S(因为拟合较自相关函数的实验曲线困难，所以本文不采用) 。峰值位置D = Dx = d0 (1+ P2/ r(P1) )。由于d0和P2为已知的实验值故可以得到r(P1)的值。
n由正文公式(9)可以求出r(P1)的误差值，由正文公式S=lP2/pW(P1)求出W(P1)，将r(P1)和W(P1)的值代入正文公式(4)和(5)就可以求出高斯光束的束腰位置P1和W02。测量误差也可以利用以上三个公式推出。
7、实验环境要求
1. 测试环境无影响测试准确度的机械振动和电磁干扰。
2. 器件所有光电参数需要在热平衡下进行，实验前应该预热3分钟。
3. 测试系统应接地良好。
4. 标准条件A
网友评论 已有 0 条评论，查看更多评论»