自1978年加拿大的Hill等人，在掺锗光纤中用488nm氩离子激光在光纤中产生驻波干涉条纹，首次成功写入光纤光栅以来，光纤光栅以其造价低、稳定性好等优良性能，被广泛应用于光纤通信和光纤传感等各领域。尤其是它易于集成的特性，使得全光纤一维光子集成成为可能，从而在促进光子学乃至信息科学的发展中显示出越来越重要的作用。普遍认为光纤光栅的研制成功是继掺铒光纤放大器(EDFA)之后在光纤领域的又一次重大的技术突破，并将成为光纤通信和传感发展史上的又一个里程碑。
光纤光栅可以作为一种光纤传感元件，除具有远距离传输、不受电磁干扰、信号带宽大、灵敏度高、响应速度快、动态范围宽、质轻、径细、结构紧凑、成本低、适于在高温、腐蚀性或危险性环境中使用等特点以外，还具有：
(1) 光源波长绝对调制，测量信号不受光源起伏、光纤弯曲损耗等因素的影响；
(2) 避免一般干涉型传感器中相位测量的不清晰和对固有参考点的依赖；
(3) 光栅的长度小，只有毫米级，测量值空间分辨率高；
(4) 输出线性范围宽，在10000微应变范围内波长移动与应变有良好的线性关系，频带宽，信噪比高；
(5) 能方便使用波分复用技术，利用多个光栅进行分布式测量。
因此光纤光栅传感器除了应用于航天飞行器、船舰、武器系统等军事领域外，还应用到建筑、桥梁、隧道、生物医学工程、石油、化工、核工业等电力工业中。
实验目的：
1、熟悉和掌握光纤光栅元件、尤其是光纤Bragg光栅的结构、原理及使用特点；
2、熟悉光纤Bragg光栅测量振动频率的实验系统和相关仪器；
3、掌握光纤Bragg光栅的解调原理并实现振动频率测量
实验原理：
1、光纤Bragg光栅结构
光纤Bragg光栅是一种纤芯折射率周期性调制的光栅，是一种均匀光栅，其结构见图1。
图1 光纤Bragg光栅结构图
光栅折射率分布为：
(1)
式中，
。
2、光纤Bragg光栅测量振动频率原理
根据耦合模理论，光纤Bragg光栅特征方程为：
(2)
光纤Bragg光栅温度传感模型
外界温度变化会引起光纤Bragg光栅中心波长发生漂移。从物理本质看，主要是由于光纤热膨胀效应、光纤热光效应及光纤内部热应力引起的弹光效应所导致。
根据光纤Bragg光栅特征方程，当外界温度发生变化时，进行展开可得：
(3)
式中，
表示温度变化量；
表示光纤直径变化量；
代表光纤光栅的热光系数；
代表热膨胀引起的弹光效应；
表示由于热膨胀导致光纤芯径变化而产生的波导效应；
表示光纤的线性膨胀系数。
对于掺锗或纯石英光纤，光纤内部热应力引起的弹光效应及波导效应比光纤热膨胀效应和光纤热光效应低几个数量级，因此造成的波长漂移量极小，可以忽略。那么方程(3)两边同除以
并简化可得：
(4)
掺锗石英光纤的热光系数
约为
，热膨胀系数
约为
，对于1550 nm波长的输入光下，单位温度变化所引起的波长漂移为10.618 pm，温度灵敏度为
/oC。可见，在无应变作用时，Bragg 波长漂移与温度变化成线性关系。
光纤Bragg光栅应变传感模型
在所有引起光纤Bragg光栅波长漂移的外界因素中，应变参量是最直接的因素之一。无论光栅受到何种力的作用，都将转化为应变作用，导致光栅物理结构周期
的变化，并且由于光纤本身的弹光效应而导致有效折射率
变化，从而引起波长漂移。
根据光纤Bragg光栅特征方程，在轴向或纵向当外界应变发生变化时，进行展开可得：
(5)
式中，
表示光纤纵向伸缩量；
代表光纤的弹光效应；表示光纤芯径变化而产生的波导效应。
根据相对介电抗渗张量与某一方向的折射率的关系、应变定义和物理条件，同时引入材料的弹光系数
整理可得：
(6)
式中，
，为有效弹光系数。
对于掺锗石英光纤，
，
，
，
，因此
。对于1550nm波长的输入光下，每个微应变所引起的波长漂移为1.209pm，应变灵敏度为0.78/
。所以恒温条件下中心波长漂移与轴向应变呈理想线性关系。光纤Bragg光栅所允许的应变可达到1％，即104 ，当超过5％时，光纤发生断裂。
3、光纤Bragg光栅中心波长解调方法
边缘滤波法是选择利用比光纤Bragg 光栅的反射谱宽度更宽的波长滤波器件对光纤Bragg 光栅反射光进行滤波，把光栅的波长信号解调为滤波器的光强信号，通过探测滤波后得到的光强计算得到波长值。解调原理见图2所示，可以看出，滤波器件的透射率曲线在一定波长范围上有一个较宽的斜坡，在工作范围内，该斜坡可视为线性，而光纤Bragg 光栅的波长在此范围内。当光纤Bragg 波长的中心波长从
移动到
时，则透过滤波器的光强发生变化变化
，通过光电二级管检测对应光栅波长漂移前后的光强，可获得波长变化的信号。
此解调方法基于波长转化为光强检测，是一种全光纤的解调方法，适用于静态和动态传感光栅波长的解调。在静态测量中，需要标定基准Bragg 波长以及单位波长变化引起的光强变化。
用于该方法的滤波器主要是长周期光纤光栅(LPG)和波分复用器(WDM)。WDM 为光通信领域中常用器件，能够将一路光信号在波长域上分为多路，因此该器件的透射率曲线上包含了多个斜坡，可对多路光纤Bragg 光栅的反射光信号解调，即波分复用技术实现多光栅传感测量。
图2 基于边缘滤波解调FBG波长的原理示意图
4、光纤Bragg光栅测量振动频率原理
光纤Bragg光栅除了实现对静态应变传感外，也可用于动态测量。光纤Bragg光栅对动态参量的响应受到传感器本身响应频率和解调系统响应的影响。
光纤Bragg光栅受到振动作用时，中心波长会随着振动频率的不同而发生相应的频率响应，因此中心波长的解调与检测成为振动测量中的重要环节。需要解调系统响应频率远高于被测量对象的振动频率。
为有效地获得光纤Bragg光栅中心波长漂移量，采用基于密集波分复用器(DWDM)器件的边缘滤波法进行解调，因为DWDM测量波长漂移具有多通道、动态测量的优点。
不同波长的光经DWDM后，其透过率不同，其解调原理如图3所示。在光纤Bragg光栅反射光脉冲宽度极小以及波长漂移量也较小的情况下，DWDM边缘滤波器输出光强变化量ΔE与光纤Bragg光栅中心波长漂移量Δλ成如下线性关系：
(7)
式中，K0为DWDM某通道滤波曲线的斜率。
经DWDM滤波后的光纤Bragg光栅反射光强被光电接收管(PIN)接收并转换为电流信号，同时在PIN管两输出端上接转换电阻，把电流信号转换为电压信号。其电压与光功率的关系为：
(8)
式中，KPIN表示PIN管的灵敏度。
图3 基于DWDM边缘滤波解调FBG波长的原理图
根据方程(6)~(8)，可知电压差值与应变关系式为：
(9)
式中，Kε为电压和应变的转换率。
对电压进行快速傅立叶变换(FFT)，其响应频率为被测量对象的振动频率，频率表达式为：
(10)
实验装置：
图4为FBG测量悬臂梁模态频率的试验装置图。放大自辐射源(ASE)发出的宽谱光经过环形器(Circulator)入射到贴在悬臂梁上的光纤Bragg光栅传感器。对满足Bragg条件的光就会被反射回环行器，然后送入DWDM进行解调。解调获得的信号通过光电接收管(PIN)转换，并使用数据采集卡(DAQ)和信号调理电路(Amplifier)对信号进行采集、处理、放大。
系统中使用压电式加速度传感器(AT)同时进行测量，从加速度传感器获得的电荷信号经转换为电压信号进行放大，利用数据采集卡(DAQ)高速采样。然后与光纤Bragg光栅传感器采集到的数据一并接入计算机(Computer)，进行处理、显示和存储。
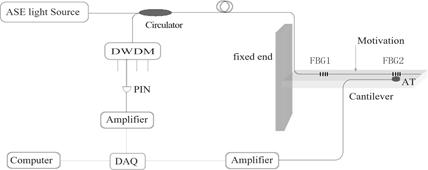
图4 光纤Bragg光栅测量悬臂梁模态频率的试验装置图
本实验采用LabVIEW软件对振动信号进行采集、处理和显示等处理。
实验步骤：
1、根据实验方案搭建测试系统，观察是否有信号输出，确保系统工作正常；
2、用光谱分析仪分析光纤Bragg光栅的初始中心波长，确定DWDM的滤波通道；
3、利用LabVIEW编数据采集、处理、显示等程序；
4、进行振动频率测量，并重复多次。
思考题：
1、如何确定光纤Bragg光栅的中心波长和DWDM的滤波通道，确保波长匹配实现正确解调？
2、如何利用波分复用方法进行多路同时测量？
3、能否利用其他的解调方法实现光纤Bragg光栅中心波长的动态解调，实现动态测量？
网友评论 已有 0 条评论，查看更多评论»